Introduzione

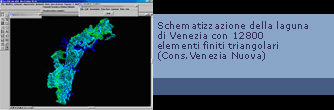
Schematizzazione della laguna

Il problema più importante per ottenere risultati significativi dalle applicazioni dei modelli matematici consiste nel determinare il numero degli elementi finiti da utilizzare nella schematizzazione del sistema idrodinamico. Si scontrano in particolare due esigenze contrastanti: la prima di aumentare quanto possibile le dimensioni degli elementi finiti e diminuire il numero dei nodi in cui viene calcolata la soluzione, per non appesantire eccessivamente lo sforzo computazionale richiesto; la seconda di aumentare il numero degli elementi finiti e dei punti di calcolo, per simulare con maggior dettaglio e precisione la situazione della laguna reale. Per soddisfare contemporaneamente entrambe le necessità, la laguna di Venezia è stata schematizzata mediante 12800 elementi finiti triangolari, corrispondenti ad una semina di oltre 7000 nodi.

La maglia degli elementi finiti è stata quindi perfettamente adagiata ai contorni reali dei canali, delle isole e dei contorni esterni della laguna, consentendo in questo modo sia una rapida distinzione della tipologia degli elementi sia una conseguente attribuzione di parametri caratteristici, quali batimetria e scabrezza. Al fine di assegnare le quote degli elementi finiti, una particolare procedura presente tra i comandi del preprocessore PreLag ha permesso di quotare le profondità degli elementi finiti in modo perfettamente aderente alla realtà lagunare, sulla base delle misure di profondità effettivamente rilevate nelle campagne di misura più recenti eseguite.

Ai fini di una corretta interpretazione delle caratteristiche di resistenza alla propagazione della marea nella laguna, gli elementi finiti triangolari sono stati suddivisi in tre diverse tipologie (laguna, canale, barena). Tenendo conto di considerazioni di carattere essenzialmente idraulico, sono stati assunti dei coefficienti di resistenza al moto differenziati per i tre diversi sistemi di elementi sopra accennati, assegnando per essi valori compresi nell'ambito di quelli generalmente accettati nell'idraulica classica per campi di moto con fondali analoghi a quelli riscontrati in laguna.

Verifica dei risultati forniti dal modello MfhLag

La verifica dei risultati forniti dal modello MfhLag è stata realizzata considerando l'evento di marea del periodo 1-6 Ottobre 1986, durante il quale erano stati registrati gli andamenti dei livelli in numerose stazioni di misura disseminate nell'intero bacino lagunare.

Dopo aver effettuato il processo di verifica con il modello idrodinamico, eseguendo numerose prove di sensibilità con l'utilizzo di diversi valori dei coefficienti di scabrezza, si é deciso di confermare i valori di 30, 35, 20 [m1/3 s-1] nella formula di Gauckler-Strickler per i sistemi di elementi laguna {1}, canale {2} e barena {3} rispettivamente.

Per fornire un esempio dei risultati ottenuti, nelle figure 3÷8 sono rappresentati i confronti tra i valori misurati e quelli simulati, durante i giorni 1÷3 Ottobre 1996, per 6 diverse stazioni di misura:

1 - Cason Figheri;

2 - Torson di Sotto;

3 - Fusina;

4 - Punta Salute;

5 - S. Erasmo;

6 - Val Dogà.

Queste stazioni idrometriche, ubicate a notevole distanza tra di loro ed appartenti ai tre diversi bacini afferenti le bocche di porto di Chioggia, Malamocco e Lido (fig. 2), possono, per questo motivo, essere considerate estremamente significative al fine di dimostrare l'eventuale capacità, da parte del modello matematico, di simulare i processi idrodinamici propagatori della marea in tutto il sistema lagunare.

I confronti tra i valori simulati e quelli misurati confermano l'ottima accuratezza con cui sono simulati i livelli relativi a tutte le stazioni di misura.

Un ulteriore aspetto, decisivo per provare la consistenza dei risultati ottenuti é costituito dalla capacità di MfhLag di conservare, entro il sistema idrodinamico lagunare, il volume di acqua entrato dalle bocche. A questo proposito nelle fig. 9 e 10 sono stati rappresentati i valori di alcune variabili, determinanti per valutare la precisione con cui MfhLag é in grado di risolvere l'equazione di conservazione della massa. In particolare, nella fig. 9 sono riportati, a confronto, i flussi entranti, complessivamente, dalle bocche a mare e la contemporanea variazione del volume di acqua in laguna, nell'unità di tempo, mentre nella fig. 10 sono confrontati i grafici dei volumi totali entrati dalle bocche e quelli variati in laguna, calcolati, cumulativamente, a partire dall'inizio della simulazione.

Nella fig. 9 il volume "Entrato Bocche" viene determinato valutando dapprima la portata complessiva che entra dalle bocche a mare, in corrispondenza di un certo istante di calcolo, moltiplicando poi tale valore per il passo temporale di calcolo del modello (pari a 180 [s]); il volume "Variazione Laguna" viene calcolato valutando prima la variazione di volume subita, durante lo stesso passo temporale di calcolo, dai singoli 12800 elementi finiti in cui é stato suddiviso il bacino lagunare e sommando poi tutti i contributi degli stessi elementi.

Questi risultati ottenuti forniscono la prova definitiva sulla precisione dei risultati forniti dal modello idrodinamico MfhLag. Infatti, considerando che l'oscillazione dello specchio liquido lagunare risulta essere, in ogni punto e in ogni istante, quasi aderente ai livelli forniti dal modello (fig. 3÷8), la precisione con cui viene conservata la massa nel bacino lagunare garantisce, altresì, l'altrettanto perfetta coincidenza tra il campo delle velocità, medie sulla verticale, ottenuto e quello realmente presente in laguna.

Conclusioni

BIBLIOGRAFIA

[1] Garzon, A., "Modello idrodinamico 2-D agli elementi finiti: Documentazione Scientifica", Studio A.2.8, Consorzio Venezia Nuova, Luglio 1988.

[2] Garzon, A., CREA s.r.l., "Taratura e calibrazione del modello idrodinamico 2-D agli elementi finiti", Consorzio Venezia Nuova, Gennaio 1995.

[3] Garzon, A., Cecconi, G., "A Two Dimensional Semi-Implicit Finite Element Model for Tidal Propagation in the Venice Lagoon", Proceedings of the Ninth International Conference on "FINITE ELEMENTS in FLUIDS, New Trends and Applications", Venezia, 15-21 Ottobre 1995.

[4] "Sezione di lavoro 20 - Batimetria della laguna. 2° stralcio: studio dell'evoluzione morfologica - Rapporto Finale", Consorzio Venezia Nuova, 1994.